Zut – le roulement est endommagé ! Si vous considérez que les roulements sont soumis à une pression et à un cisaillement continus, cela n’a rien d’inhabituel. Ce qui est déterminant, c’est plutôt le moment où le roulement va défaillir. Le calcul de la durée de vie est d’une importance capitale pour le dimensionnement d’un palier et pour que la défaillance du roulement ne soit pas imprevisible et puisse être évitée. La vie d’un roulement n’est pas exprimée en années, mais en nombre total de tours ou d’heures de fonctionnement théoriquement possibles avant l’apparition d’une défaillance par fatigue du matériau.
La durée de vie nominale L10
La durée de vie des roulements la plus connue, souvent appelée « durée de vie catalogue », est désignée par L10 et est normalisée selon la norme DIN 281:2007 (formule de calcul, voir ci-dessous). La condition pour atteindre la durée de vie calculée est une estimation réaliste des conditions de fonctionnement telles que la vitesse de rotation, la charge et les conditions ambiantes.
| L10 | Durée de vie nominale en 106 rotations | |||
| L10h | Durée de vie nominale en heures de fonctionnement | |||
| C | Charge dynamique de base selon le tableau (voir par ex. le catalogue NTN (Cr : charge radiale, Ca : charge axiale) | |||
| P | Charge dynamique équivalente (Pr : charge radiale, Pa : charge axiale) | |||
| p | Exposant de durée de vie (roulement à billes: p = 3, roulement à rouleaux: p = 10/3) | |||
| n | Vitesse de rotation du roulement dans l’application, min.-1 | |||
Étant donné que les roulements diffèrent légèrement les uns des autres en raison des tolérances de fabrication et de la nature des matériaux, un groupe de roulements du même type dans les mêmes conditions de fonctionnement (même vitesse, charge et lubrification) présente en réalité une durée de vie variable. Ce que l’on appelle la plage de dispersion ressemble à une indication de probabilité, car elle est déterminée statistiquement. La durée de vie statistique (la durée de vie nominale L10 selon la norme DIN ISO 281:2007) indique le nombre total de rotations en millions de tours, atteint par 90 % des roulements d’un groupe identique jusqu’à ce qu’une fatigue du matériau se produise. Ceci est valable dans des conditions de fonctionnement identiques à une vitesse de rotation constante.
La réponse à la question « pourquoi seulement 90 % ? » est simple : l’exploitation d’une installation respectant à 100 % la durée de vie calculée serait tout simplement trop chère. La plage de dispersion de 90 % signifie en même temps que les 10 % restants « peuvent » tomber en panne avant la date indiquée. Le calcul de L10 se distingue par l’exposant, selon le type de roulement : à billes ou à rouleaux. La durée de vie nominale L10h permet d’indiquer le nombre d’heures de fonctionnement réalisables (formule 1).
Formule 1
Durée de vie en 106 rotations :
pour les roulements à billes : L10 = (C/P)3
pour les roulements à rouleaux : L10 = (C/P)10/3
Durée de vie en heures de fonctionnement :
L10h = (16 666,6 ̅/n) x (C/P)p
Pour les roulements à billes, si l’on divise la charge par deux ou si l’on double la charge de base, on multiplie la durée de vie par huit.
Les exigences les plus sévères en matière de durée de vie des roulements se retrouvent dans l’énergie éolienne, les moteurs électriques et les machines-outils. Dans les applications agricoles, où certaines machines ne sont utilisées que de manière saisonnière, une durée de vie moins élevée est calculée – en effet, la pollution et les conditions extérieures jouent ici un rôle important qui ne peut pas toujours être représenté par le calcul.
La durée de vie nominale en heures L10h
La charge dynamique de base C, spécifique au roulement, est importante pour le calcul de L10h. Elle indique la capacité de charge des roulements et, par conséquent, la charge dynamique qu’un roulement peut supporter. Le calcul de la charge dynamique de base est également normalisé selon la norme DIN 281:2007 et est indiqué par le fabricant de roulements dans son catalogue pour les roulements standard. Lorsque le roulement est soumis à une charge correspondant à la charge dynamique de base, le roulement atteint en théorie une durée de vie d’un million de rotations. Dans la pratique, il convient toutefois de respecter ou de vérifier d’autres conditions… D’ailleurs, on indique dans la charge de base dynamique, seule la direction de charge radiale pour les roulements radiaux, et seule la direction de charge axiale pour les butées,. C’est la raison pour laquelle on différencie les désignations Cr pour les roulements radiaux et Ca pour les butées.
Pour de nombreux roulements, la charge F s’applique au roulement suivant un angle. Il en résulte alors une force radiale Fr et une force axiale Fa. Pour calculer la durée de vie nominale, on suppose toutefois que la charge est de valeur et de direction constantes. C’est pourquoi la charge dynamique équivalente du roulement est déterminée à partir des deux forces, appelée charge radiale dynamique équivalente (Pr) pour les roulements radiaux et charge axiale dynamique équivalente (Pa) pour les butées. Lorsque le roulement est soumis à cette charge équivalente calculée, il atteint la même durée de vie L10 que dans les conditions de charge réelles.
Cette formule permet de calculer la charge dynamique équivalente .
De plus, les roulements doivent fonctionner avec une charge minimale afin de garantir un rotation sûre des corps roulants et de minimiser les glissements. Ces derniers doivent être évités afin d’empêcher l’usure (c’est-à-dire la formation de dépôts de matière et l’apparition d’une surface de roulement rugueuse), car cela peut entraîner une défaillance prématurée du roulement. La charge minimale recommandée varie selon le type de roulement et devrait être de 0,01 x C0 pour les roulements à rotule sur rouleaux, par exemple.
L’exposant de durée de vie p est déjà défini, une formule n’est donc pas nécessaire. La seule chose dont il faut tenir compte est le type de roulement dont la durée de vie doit être calculée. Ainsi, l’exposant de durée de vie des roulements à billes a une valeur de p = 3, tandis que celui des roulements à rouleaux est de p = 10/3 .
Exemple de calcul de L10 et L10h
Roulement : 6206C3
Cr = 21,6 kN
Fa = 250 N
Fr = 2 000 N
n = 2000 U/min
X = 1, Y = 0, da Fa/Fr ≤ e
Pr = 2 kN
L10 = (21,6/2)3 = 1 259,71 x 106 tours
L10h = 10 497,6 h
Un calcul de L10 et L10h sur l’exemple du roulement à billes à gorge profonde 6206C3.
La durée de vie modifiée étendue Lnm ou Lnmh
Bien que la plage de dispersion de la durée de vie nominale L10 soit basée sur un coefficient de fiabilité de 90 %, il existe certains domaines d’application dans lesquels celui-ci doit être plus élevé. C’est alors qu’intervient la durée de vie étendue Lnm ou Lnmh, également normalisée selon la norme DIN ISO 281:2007, dont on ne peut se passer dans certains cas lors du calcul de la durée de vie.
Formule 3
Lnm = a1 x aISO x L10
Lnmh = a1 x aISO x L10h
| Lnm | Durée de vie étendue en 106 tours |
| Lnmh | Durée de vie étendue en heures |
| a1 | Coefficient de durée de vie pour la fiabilité |
| aISO | Coefficient de durée de vie pour les conditions de fonctionnement aISO = f (ec × Cu ÷ P, κ) ec = Coefficient de pollution Cu = Charge limite de fatigue P = Charge dynamique équivalente κ = Rapport de viscosité |
| L10 | Durée de vie nominale : durée de vie de référence en 106 tours |
Pas de piège ici, le calcul modifié de la durée de vie des roulements Lnm et Lnmh reste des mathématiques simples. Il faut toutefois faire quelques calculs préalables, notamment pour aISO .
L’expérience montre que les roulements peuvent tout à fait dépasser les valeurs calculées dans des conditions de fonctionnement idéales, par exemple, avec un film lubrifiant entre les corps roulants et les bagues, sans salissures ni impuretés. Il est à noter que des durées de vie très élevées soient possibles jusqu’à atteindre la limite de résistance en fatigue. Les conditions pour cela sont un fonctionnement optimal et une faible charge du roulement. Avec une pression de contact maximale de 1500 MPa, le roulement est généralement considéré comme résistant à la fatigue (charge du roulement inférieure à la charge limite Cu). La durée de vie modifiée étendue fournit donc des résultats plus précis et plus proches de la réalité que la durée de vie nominale.
Pour a1, on suppose en principe une probabilité de défaillance de 10 %. Pour cette raison, a1 = 1 et la valeur de a1 est donc modifiée pour une autre probabilité de défaillance.
| Fiabilité | Ln | Coefficient de fiabilité a1 |
| 90 % | L10 | 1,00 |
| 95 % | L5 | 0,62 |
| 96 % | L4 | 0,53 |
| 97 % | L3 | 0,44 |
| 98 % | L2 | 0,33 |
| 99 % | L1 | 0,21 |
Le coefficient de fiabilité a1 diminue lorsque le pourcentage de fiabilité de l’indication de durée de vie augmente.
Le facteur aISO est une fonction basée sur la lubrification, la pollution, les propriétés du matériau ainsi que la charge, et peut être décrite par la formule suivante :
La pollution due à des particules dures dans le lubrifiant peut provoquer des creux à la surface du chemin de roulement, ce qui se traduit par une surface endommagée et une réduction de la durée de vie du roulement. Le coefficient de contamination eC en tient compte et dépend du degré de pollution, de la taille du roulement et de la viscosité du lubrifiant (épaisseur du film lubrifiant).
| Coefficient de contamination | ec | |
Dpw < 100 mm | Dpw ≥ 100 mm | |
Propreté la plus élevée Taille des particules de l’ordre de l’épaisseur du film lubrifiant ; conditions en laboratoire | 1 | 1 |
Propreté élevée Huile filtrée par un filtre extrêmement fin ; conditions typiques pour des roulements lubrifiés à vie avec joints d’étanchéité | 0,8 ~ 0,6 | 0,9 ~ 0,8 |
Propreté normale Huile filtrée par un filtre fin ; conditions typiques des roulements lubrifiés à vie avec des déflecteurs | 0,6 ~ 0,5 | 0,8 ~ 0,6 |
Contamination légère Légère contamination du lubrifiant | 0,5 ~ 0,3 | 0,6 ~ 0,4 |
Contamination typique Conditions typiques pour les roulements sans joints d‘étanchéité ; filtration grossière ; particules d’usure et pollution provenant de l’environnement | 0,3 ~ 0,1 | 0,4 ~ 0,2 |
Forte contamination Environnement du roulement fortement pollué et montage du roulement avec étanchéité inadéquate | 0,1 ~ 0 | 0,1 ~ 0 |
| Très forte contamination | 0 | 0 |
Le tableau décrit le degré de contamination ec.
La charge limite en fatigue est un autre facteur influent. Elle correspond à la charge exercée sur un roulement qui conduit à la contrainte limite en fatigue, situé au contact le plus chargé à l’intérieur du chemin de roulement. Cette charge limite en fatigue dépend du type de roulement, des spécifications internes, de la qualité et de la résistance du matériau. Dans la norme ISO 281:2007, une contrainte de contact de 1,5 GPa, correspondant au Cu, est recommandée pour les roulements en matériaux de haute qualité et avec un bon niveau de fabrication.
En outre, le rapport de viscosité κ, qui décrit l’influence de la formation du film lubrifiant, est intégré dans aISO. Les roulements sont utilisés en supposant que les surfaces de contact du roulement sont séparées par un film lubrifiant. Cependant, si la viscosité du lubrifiant est faible, la séparation devient insuffisante et un contact direct métal/métal se produit, entraînant un endommagement. Le rapport de viscosité κ tient compte de cet effet, décrit ci-dessous, par le rapport entre la viscosité de fonctionnement v et la viscosité de référence v1 .
Formule 4
κ = v/v1
Le calcul du rapport de viscosité κ.
Formule 5
Si n < 1 000 min-1, v1 = 45 000 n-0,83 Dpw-0,5
Si n ≥ 1 000 min-1, v1 = 4 500 n-0,5 Dpw-0,5
La viscosité de référence v1 dépend de la vitesse de rotation n et de la valeur de Dpw.
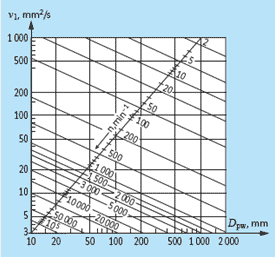
Calcul de la viscosité de référence v1 au moyen d’un diagramme.
Les diagrammes illustrent la relation entre Cu/P, ec, κ et aISO de différents types de roulements. L’utilisation des diagrammes est soumise aux restrictions suivantes : le coefficient de durée de vie est limité à aISO ≤ 50 et, si κ > 4, alors on prendra la valeur de κ = 4. De plus, l’approche n’est pas valable pour κ < 0.1.
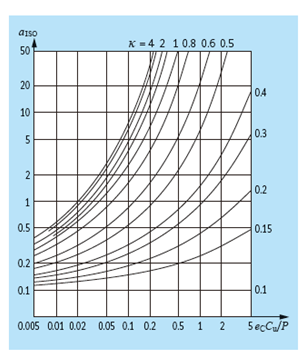
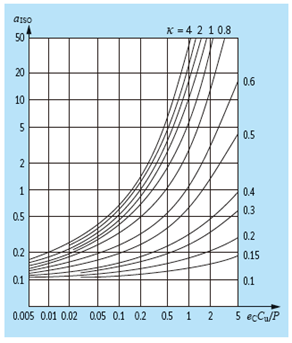

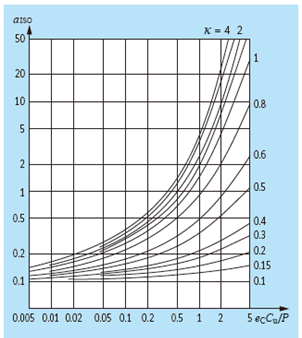
De haut en bas et de gauche à droite, vous trouverez des indications sur le coefficient de durée de vie aISO des roulements à billes radiaux, des roulements à rouleaux radiaux, des butées à billes et enfin des butées à rouleaux.
Exemple de calcul de L10mh
Même roulement et application que ci-dessus : 6206C3
Cr = 21,6 kN
Cu = 0,795 kN
Fa = 250 N
Fr = 2 000 N
n = 2 000 tr/min
Propreté élevée de l’environnement
Viscosité du lubrifiant à la température de fonctionnement de 80°C de 14,37 mm²/s
X = 1, Y = 0, da Fa/Fr ≤ e
Pr = 2 kN
L10 = (21,6/2)3 = 1 259,71 x 106 tours
L10h = 10 497,6 h
Avec Dpw < 100 mm il en résulte eC = 0,6 – 0,8
Avec la formule 5, on obtient pour v1 = 14,76 mm²/s
Il en résulte κ = 0,9
Le diagramme pour les roulements à billes radiaux permet de déduire pour aISO une valeur d’environ 8
Il en résulte pour L10hm = 83 981 h
Exemple de calcul de L10mh pour le roulement à billes à gorge profonde 6206C3.
Autres méthodes de calcul de la durée de vie des roulements
En plus des méthodes présentées ici pour déterminer la durée de vie d’un roulement, il en existe d’autres en lien avec la défaillance due à la fatigue du matériau. Ainsi, dans le calcul de la durée de vie de référence selon la norme ISO TS 16281, la répartition de la charge du corps roulant sur sa longueur est considérée à l’aide d’un modèle par tranches. Cette méthode prend en compte d’autres facteurs influents tels que le jeu de fonctionnement et le désalignement du roulement, mais aussi les pressions de contact existantes des différents éléments du roulement. En raison de l’immense travail de calcul, une telle méthode ne convient toutefois que si l’on utilise un programme de calcul.
Vous pourriez également être intéressé par
Lubrification
Rien ne fonctionne sans lubrification : chaque roulement nécessite un lubrifiant de type graisse ou huile, condition de base pour éviter tout contact métallique entre




